코딩테스트 풀이
프로그래머스 코딩테스트
hanlabong
2025. 1. 9. 21:32
728x90
문제
https://school.programmers.co.kr/learn/courses/30/lessons/42839#
[프로그래머스
SW개발자를 위한 평가, 교육, 채용까지 Total Solution을 제공하는 개발자 성장을 위한 베이스캠프
programmers.co.kr](https://school.programmers.co.kr/learn/courses/30/lessons/42839#)
해결 방법
아이디어
- 완전 탐색으로 가능한 모든 숫자 찾기
- 숫자를 하나씩 탐색
- 숫자가 소수라면
- 이미 탐색한 숫자가 아니라면
- count up
- 이미 탐색한 숫자가 아니라면
- 숫자가 소수라면
소수 확인
function isPrime(number) {
if (number < 2) return false;
for (let i = 2; i <= number ** 0.5; i++) {
if (number % i === 0) {
return false;
}
}
return true;
}- parameter
- number
- type: number
- 소수인지 확인할 숫자
- number
- return
- type: boolean
- true: 소수
- false: 소수 아님
중요한 점
- 2 미만은 소수가 아니다.
- 소수는 2부터 시작이다.
- number보다 작은 모든 수를 사용해 소수인지 확인할 필요가 없다.
- number = a * b라고 했을 때 a와 b 중 최솟값은 number 의 제곱근을 넘지 않는다.
- 따라서 반복문은 number 의 제곱근까지만 반복하면 된다.
재귀 함수
완전 탐색 재귀 함수
function getNumber(numbers) {
if (numbers.length === 1) return numbers;
return numbers
.map((num, index) => // numbers를 순회하며
getNumber(numbers.filter((_, idx) => idx !== index)) // 현재 num을 제외한 배열의 숫자 조합
.map((n) => [num + n, n]) // 그 결과를 순회하며 num과 숫자(n)를 결합한 값과 n을 배열로 반환
.flat() // 2차원 배열을 1차원으로 변환
)
.flat(); // 2차원 배열을 1차원으로 변환
}- parameter
- numbers
- type: string[]
- 순회하며 숫자를 조합할 배열
- numbers
- return
- type: string[]
- 조합된 숫자 배열
과정이 복잡해서 그려본 numbers가 “123”이라고 했을 때 조합을 찾는 과정

전체 코드
function isPrime(number) {
if (number < 2) return false;
for (let i = 2; i <= number ** 0.5; i++) {
if (number % i === 0) {
return false;
}
}
return true;
}
function getNumber(numbers) {
if(numbers.length === 1) return numbers
return [...numbers
.map((num, index) =>
getNumber(numbers.filter((_, idx) => idx !== index)).map((n) => [num + n, n])
.flat())
].flat()
}
function solution(numbers) {
var answer = [];
const resultArr = [];
const numArr = numbers.split("");
const result = getNumber(numArr)
for (let i = 0; i < result.length; i++) {
const num = Number(result[i])
if (!resultArr.includes(num)) {
resultArr.push(num);
if (isPrime(num)) {
answer.push(num)
}
}
}
return answer.length;
}Set을 활용하자
var answer = new Set();
function getCombi(arr, str) {
if (arr.length > 0) { // arr에 숫자가 있을 때
for (let i = 0; i < arr.length; i++) { // arr를 순회하며
const newArr = [...arr]; // arr를 복사해 새로운 배열 생성
newArr.splice(i, 1); // i 번째 요소 제거
getCombi(newArr, str + arr[i]); // i 번쨰 요소가 제거된 배열과 i 번쨰 요소를 결합한 숫자로 조합 생성
}
}
if (str.length > 0) { // str이 빈 문자열이 아니라면
const number = Number(str); // number로 변환
if (isPrime(number)) { // number가 소수라면
answer.add(number); // answer에 number를 추가한다.
}
}
}- parameter
- arr
- string[]
- 순회하며 숫자를 조합할 배열
- str
- string
- 현재 숫자 문자열
- arr

전체 코드
function isPrime(number) {
if (number < 2) return false;
for (let i = 2; i <= number ** 0.5; i++) {
if (number % i === 0) {
return false;
}
}
return true;
}
function solution(numbers) {
var answer = new Set();
const numArr = numbers.split("");
getCombi(numArr, "")
function getCombi(arr, str) {
if (arr.length > 0) {
for (let i = 0; i < arr.length; i++) {
const newArr = arr.slice(0)
newArr.splice(i, 1)
getCombi(newArr, str + arr[i])
}
}
if (str.length > 0) {
const number = Number(str);
if (isPrime(number)) {
answer.add(number)
}
}
}
return answer.size;
}
두 방법의 차이?

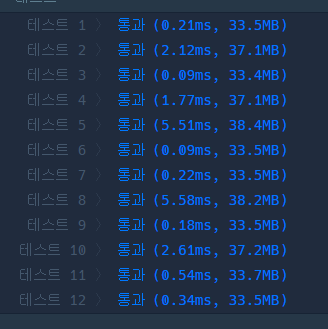
수행 시간이 절반 이상 줄어든 것을 확인할 수 있었다. ⇒ 나올 수 있는 조합의 크기가 달라지기 때문
방법 1
- “12” ⇒ 4가지
- 2 * 2
- “123” ⇒ 24가지
- (2 * 2) * 2 * 3
- “1234” ⇒ 192가지
- ((2 * 2) * 2 * 3) * 2 * 4
방법 2
- “12” ⇒ 4가지
- 2 + (1 * 2)
- “123” ⇒ 15가지
- 3 + (2 * 3) + (1 * 2 * 3)
- “1234” ⇒ 64가지
- 4 + (3 * 4) + (2 * 3 * 4) + (1 * 2 * 3 * 4)
$$ n + n(n-1) + ... + n! $$
$$ \sum^{x}_{n=1} \cfrac{x!}{(x-n)!} $$
첫 번째 방법의 경우 조합의 수가 기하급수적으로 늘어나기 때문에 시간 차이가 날 수 밖에 없다.
https://www.desmos.com/calculator/ctizmiost1?lang=ko
지수함수 그래프
www.desmos.com
728x90